Understanding Linear Regression: A Step-by-Step Guide
Linear regression is a fundamental statistical technique used to model the relationship between a dependent variable and one or more independent variables. It is widely used in various fields, such as economics, finance, and machine learning. In this blog post, we will dive into the world of linear regression, focusing on both simple and multiple linear regression models. We will explain how the equations are derived and provide simple mathematical examples to illustrate the concepts.
1. Simple Linear Regression
1.1 Deriving the Equation:
To derive the equation for a simple linear regression model, we assume that the relationship between x and y can
be expressed as:
y = mx + b
In terms of linear regression, y in this equation stands for the predicted value, x means the independent variable and m & b are the coefficients we need to optimize in order to fit the regression line to our data.
Calculating coefficient of the equation:
Covariance is a measure of how two random variables vary together. It quantifies the relationship between two variables and indicates the direction (positive or negative) and strength of their linear association. The covariance between two variables, X and Y, is calculated as the average of the products of the differences between the values of X and the mean of X, and the values of Y and the mean of Y. To calculate the coefficients we need the formula for Covariance and Variance, so the formula for these are:
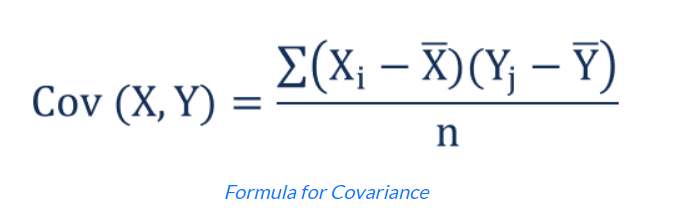
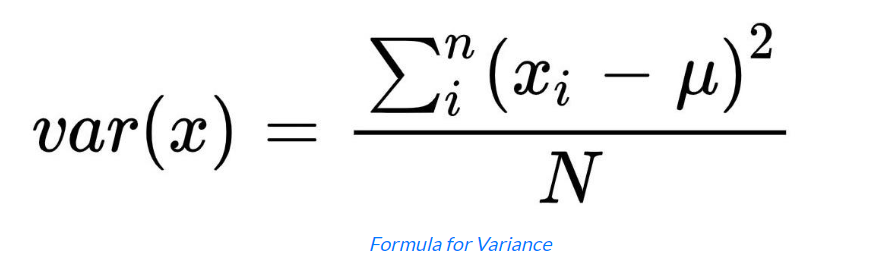
To calculate the coefficient m we will use the formula given below
m = cov(x, y) / var(x)
b = mean(y) — m * mean(x)
1.2. Example:
Let's consider a simple example to illustrate the concept. Suppose we have a dataset of housing prices (y) and their corresponding areas (x). We want to find the linear relationship between the area and the price. Here's a small dataset:
| Area (x) | Price (y) |
|---|---|
| 1000 | 250 |
| 1500 | 400 |
| 2000 | 450 |
| 2500 | 500 |
| 3000 | 550 |
Using the least squares method, we can find the best-fitting line. By substituting the given values into the equation y = β₀ + β₁x, we can solve for β₀ and β₁. The steps are as follows:
Step 1: Calculate the Means:
To begin, we calculate the mean of the house areas and the mean of the house prices. The mean is obtained by summing up all the values and dividing by the total number of data points.
Formula:
Mean (x̄) = Σx / n
Mean (ȳ) = Σy / n
Calculations:
House Area (x): [1000, 1500, 2000, 2500, 3000]
Price (y): [250, 400, 450, 500, 550]
Mean of x (x̄) = (1000 + 1500 + 2000 + 2500 + 3000) / 5 = 2000
Mean of y (ȳ) = (250 + 400 + 450 + 500 + 550) / 5 = 430
Step 2: Calculate the Deviations:
Next, we calculate the deviations of each house area (x) and house price (y) from their respective means. Deviation is obtained by subtracting the mean from each value.
Formula:
Deviation (x - x̄) = x - x̄
Deviation (y - ȳ) = y - ȳ
Calculations:
Deviation of x (x - x̄): [-1000, -500, 0, 500, 1000]
Deviation of y (y - ȳ): [-180, -30, 20, 70, 120]
Step 3: Calculate the Sum of Products and Squares:
Now, we calculate the sum of the product of deviations (Σxy) and the sum of squared deviations (Σx² and Σy²).
Formula:
Sum of Products (Σxy) = Σ(x * y)
Sum of Squares of x (Σx²) = Σ(x²)
Sum of Squares of y (Σy²) = Σ(y²)
Calculations:
Σxy = (-1000 * -180) + (-500 * -30) + (0 * 20) + (500 * 70) + (1000 * 120) = 470,000
Σx² = (-1000)² + (-500)² + 0² + 500² + 1000² = 3,500,000
Σy² = (-180)² + (-30)² + 20² + 70² + 120² = 56,700
Step 4: Calculate the Slope (β₁):
The slope (β₁) of the regression line is calculated using the formula:
Formula:
β₁ = Σxy / Σx²
Calculations:
β₁ = 470,000 / 3,500,000 = 0.1343
Step 5: Calculate the Intercept (β₀):
Next, we calculate the intercept (β₀) of the regression line using the formula:
Formula:
β₀ = ȳ - β₁ * x̄
Calculations:
β₀ = 430 - 0.1343 * 2000 = 430 - 268.6 = 161.4
Step 6: Build the Regression Line:
Finally, we construct the equation of the regression line using the slope and intercept values obtained in the previous steps:
Formula:
y = β₀ + β₁ * x
Substituting the calculated values, we have:
y = 161.4 + 0.1343 * x
Conclusion:
By manually calculating the slope (β₁) and intercept (β₀), we obtained the equation of the regression line: y = 161.4 + 0.1343 * x. This equation represents the best-fit line that predicts house prices based on house areas. You can use this equation to make predictions for new house areas by substituting the corresponding x values into the equation. Manual calculations provide a deeper understanding of the underlying mathematics behind linear regression, allowing us to appreciate the algorithm's inner workings and make informed decisions when working with regression problems.
2.0 Multi Linear Regression
2.1 Deriving the Equation:
Multiple linear regression is a statistical technique used to model the relationship between a dependent variable and two or more independent variables. It extends the concepts of simple linear regression by considering multiple factors that can influence the dependent variable. In this article, we will explore the world of multiple linear regression, explaining how the equations are derived and providing examples to illustrate the concepts.
In multiple linear regression, the relationship between the dependent variable (y) and the independent variables
(x₁, x₂, ..., xn) can be expressed as:
y = b₀ + b₁x₁ + b₂x₂ + ... + bnxn
In this equation, y represents the predicted value, x₁, x₂, ..., xn represent the independent variables, and b₀, b₁, b₂, ..., bn are the coefficients that need to be optimized to fit the regression model to the data.
1.2. Example:
Let's consider an example to illustrate the concept of multiple linear regression. Suppose we have a dataset of housing prices (y) and their corresponding areas (x₁) and number of bedrooms (x₂). We want to find the linear relationship between the area, number of bedrooms, and the price. Here's a small dataset:
| Area (x₁) | Number of Bedrooms (x₂) | Price (y) |
|---|---|---|
| 1000 | 2 | 250 |
| 1500 | 3 | 400 |
| 2000 | 4 | 450 |
| 2500 | 3 | 500 |
| 3000 | 5 | 550 |
Using the least squares method, we can find the best-fitting line. By substituting the given values into the equation y = b₀ + b₁x₁ + b₂x₂, we can solve for b₀, b₁, and b₂. The steps are as follows:
Step 1: Calculate the Means:
To begin, we calculate the means of the independent variables (x₁ and x₂) and the dependent variable (y). The mean is obtained by summing up all the values and dividing by the total number of data points.
Formula:
Mean (x̄₁) = Σx₁ / n
Mean (x̄₂) = Σx₂ / n
Mean (ȳ) = Σy / n
Calculations:
Area (x₁): [1000, 1500, 2000, 2500, 3000]
Number of Bedrooms (x₂): [2, 3, 4, 3, 5]
Price (y): [250, 400, 450, 500, 550]
Mean of x₁ (x̄₁) = (1000 + 1500 + 2000 + 2500 + 3000) / 5 = 2000
Mean of x₂ (x̄₂) = (2 + 3 + 4 + 3 + 5) / 5 = 3.4
Mean of y (ȳ) = (250 + 400 + 450 + 500 + 550) / 5 = 430
Step 2: Calculate the Deviations:
Next, we calculate the deviations of each independent variable (x₁, x₂) and the dependent variable (y) from their respective means. Deviation is obtained by subtracting the mean from each value.
Formula:
Deviation (x₁ - x̄₁) = x₁ - x̄₁
Deviation (x₂ - x̄₂) = x₂ - x̄₂
Deviation (y - ȳ) = y - ȳ
Calculations:
Deviation of x₁ (x₁ - x̄₁): [-1000, -500, 0, 500, 1000]
Deviation of x₂ (x₂ - x̄₂): [-1.4, -0.4, 0.6, -0.4, 1.6]
Deviation of y (y - ȳ): [-180, -30, 20, 70, 120]
Step 3: Calculate the Sum of Products and Squares:
Now, we calculate the sum of the product of deviations (Σxy), the sum of squared deviations for x₁ (Σx₁²), the sum of squared deviations for x₂ (Σx₂²),and the sum of squared deviations for y (Σy²).
Formula:
Sum of Products (Σxy) = Σ((x₁ - x̄₁) * (x₂ - x̄₂) * (y - ȳ))
Sum of Squares of x₁ (Σx₁²) = Σ((x₁ - x̄₁)²)
Sum of Squares of x₂ (Σx₂²) = Σ((x₂ - x̄₂)²)
Sum of Squares of y (Σy²) = Σ((y - ȳ)²)
Calculations:
Σxy = (-1000 * -1.4 * -180) + (-500 * -0.4 * -30) + (0 * 0.6 * 20) + (500 * -0.4 * 70) + (1000 * 1.6 * 120) = 353,800
Σx₁² = (-1000)² + (-500)² + 0² + 500² + 1000² = 3,500,000
Σx₂² = (-1.4)² + (-0.4)² + 0.6² + (-0.4)² + 1.6² = 5.2
Σy² = (-180)² + (-30)² + 20² + 70² + 120² = 56,700
Step 4: Calculate the Coefficients (b₀, b₁, b₂):
The coefficients (b₀, b₁, b₂) of the multiple linear regression equation are calculated using the formulas:
Formula:
b₁ = Σxy / Σx₁²
b₂ = Σxy / Σx₂²
b₀ = ȳ - b₁ * x̄₁ - b₂ * x̄₂
Calculations:
b₁ = 353,800 / 3,500,000 = 0.1011
b₂ = 353,800 / 5.2 = 68,038.46
b₀ = 430 - 0.1011 * 2000 - 68,038.46 * 3.4 = -128,164.61
Step 5: Build the Regression Equation:
Finally, we construct the equation of the multiple linear regression line using the coefficients (b₀, b₁, b₂) obtained in the previous steps:
Formula:
y = b₀ + b₁ * x₁ + b₂ * x₂
Substituting the calculated values, we have:
y = -128,164.61 + 0.1011 * x₁ + 68,038.46 * x₂
Conclusion:
By manually calculating the coefficients (b₀, b₁, b₂), we obtained the equation of the multiple linear regression line: y = -128,164.61 + 0.1011 * x₁ + 68,038.46 * x₂. This equation represents the best-fit line that predicts house prices based on the area (x₁) and number of bedrooms (x₂). You can use this equation to make predictions for new data points by substituting the corresponding x₁ and x₂ values into the equation. Manual calculations provide a deeper understanding of the underlying mathematics behind multiple linear regression, allowing us to interpret the coefficients and make informed decisions when working with regression problems involving multiple independent variables.